Cyber-T Help

Contents

• Background
• Downloading and installing Cyber-T / bayesreg.R (R code)
• Using the bayesreg.R code in R
• Input data file format
• Meanings of input parameters
• Cyber-T results
• General questions, common errors and troubleshooting
• References

Background

The Cyber-T Bayesian statistical framework was developed by Pierre Baldi and first implemented in collaboration with Tony Long [1]. The web interface was first implemented by Harry Mangalam. Cyber-T has received valuable inputs from many UCI biologists, in particular from G. Wesley Hatfield, Denis Heck, She-pin Hung, Michelle Riehle and Suzanne Sandmeyer. The program has been maintained and extended by various members of the Baldi group, including: Yann Pecout, Laurence Richard, Suman Sundaresh, Michael Zeller, and Matthew Kayala.

Cyber-T has been ranked by investigators from Harvard University and the Pasteur Institute as the best commercial or public software package for the analysis and interpretation of DNA microarray data [2]. The superiority of Cyber-T was further demonstrated in other comparison experiments [3-5].

In addition to DNA microarray analysis [6-8], Cyber-T has been used to analyze other high-throughput data, including protein microarrays [9,10] and quantitative mass spectrometry data (for example [11]). Current works in press use Cyber-T for the differential analysis of Next Generation Sequencing data (RNA-Seq, ChIP-Seq, etc).

Downloading/Installing Cyber-T R Code

***NEW: Newly written Cyber-T library (bayesreg.R) available for download.***

Download here!

The new version includes paired and unpaired t-tests, one-way ANOVA, and all recent improvements such as extreme low replication handling, normalization, and post-processing options.

Cyber-T and/or the R library (including the old hdarray and new bayesreg.R) is free for academic, non-commercial, research use only. The appropriate references [1] should be cited when used for academic/research purposes. For commercial licenses, please contact IGB Licences.

To work with the Cyber-T library written in R directly, you need to have R installed. There are installation packages available for most platforms and source code that will compile with gcc, all available via your nearest node of the Comprehensive R Archive Network.

Assuming you have R installed on your system, just 'source' the bayesreg.R file using either the command line interface or the menu.

What is in the Cyber-T library (bayesreg.R)?

• bayesT : main function for unpaired two-sample t-tests (both Bayesian and non-Bayesian versions)
• bayesT.pair : main function for paired two-sample t-tests (both Bayesian and non-Bayesian versions). A paired test is appropriate when controls and experimentals are paired. An example of this is "Brown-type" array data where each control has a matching experimental treatment.
• runAllBayesAnova : main function for the one-way ANOVA (both Bayesian and non-Bayesian versions). An ANOVA is appropriate when there are more than two experimental conditions to analyze. An example of this would be array data from more than two different types of tissue.
• ppdeMix : main function for running Posterior Probability of Differential Expression analysis.
• runVsn : main function to run Variance Stabilizing Normalization (VSN) pre-processing. Note: The 'vsn' package from Bioconductor must be installed.
• runMulttest : main function to calculate Bonferroni and Benjamini & Hochberg multiple hypothesis testing correction. Note: The 'multtest' package from Bioconductor must be installed.
• postHoc : main function to run postHoc tests for the one-way ANOVA.
• cyberTPlots : main function for plotting the basics of the data. The 'lattice' package must be installed.

The bayesreg.R file is well commented. It should be easy to use with a minimal knowledge of R.

Using the bayesreg.R code in R

Depending on what platform you are running the R code, you need to use the menu options and 'source' the bayesreg.R file. This loads all the functions in hdarray in to R. On Windows or Unix-like systems, you can type "source(filename)" at the command line. You may also want to use the menu option to change the R working directory to the directory that contains your data. Let's assume a simple text file 'Expt1.txt' as follows:

      C1,C2,E1,E2
      gene1,10,8,7,9
      gene2,6,5,7,6
      gene3,4,5,8,9

The following commands demonstrate how to read a data file and invoke the various functions to perform t-tests or bayes-t-tests on either paired, unpaired, multiple conditions data. The R command line prompt may look like this ">" after which you can type the commands shown below.

Read the data file which, in this case, is comma separated. If the file is tab separated, ignore the 'sep' field. Do not type the ">". If the data file is not in your working directory, you need to specify the full file path.
Tab delimited file:
> dataFile<-read.table("Expt1.txt")
Comma delimited file:
> dataFile<-read.table("Expt1.txt",sep=",")
Space delimited file:
> dataFile<-read.table("Expt1.txt",sep=" ")

Display the first row to make sure the file has been read correctly
> dataFile[1,]

      C1 C2 E1 E2
      gene1 10  8  7  9  

As you can see, the file has been read correctly. Since the first line had column names, the file was read correctly as the header. Note that there is no header name for the gene name column hence the gene name column is used to label the rows. If you don't have the column names, it works just fine too. R will create its own column names.

Display the dimensions of the dataset. The first number is the number of rows, the second is the number of columns.
> dim(dataFile)

      [1] 3 4 

Now that the data has been read, we can proceed to apply the various functions. Let's apply the standard unpaired t-test (with bayesT and appropriate parameters).
> bayesT(dataFile,numC=2,numE=2,ppde=0,bayes=0)

The outputs of the code are exactly the outputs from the webserver. All parameters in the functions correspond with form elements on the webserver (and are documented in the code comments).

That's it! When you apply the commands above, the data file gets processed and some output files - allgene.txt, ROC.txt, mix.txt and several png files - are saved in your working directory. 'allgene.txt' contains all the analysis output data. 'png' files contain supporting graphs, 'mix.txt' contains the mixture model parameters, and 'ROC.txt' contains the x and y-coordinates for the ROC plot in temp.ps. Note: some of these files may not get generated depending on the parameters used. See the Cyber-T results section for details.

File Format

The format expected is essentially the output of a spreadsheet file in ASCII or plain text with the values delimited by tabs, commas, or spaces. If your data are in Excel or a similar spreadsheet program, they should be saved as text files and delimited by tabs, commas, or spaces. Make sure that your labels (gene names) do not include whatever you choose.

Comments can be inserted anywhere in the text as long as the comment lines are prefixed by a '#' because the underlying R code will ignore command lines beginning with #. Column headings must be removed unless they are preficed by a # sign or specifically excluded by identifying which is data start row. Do note that having the # sign in the middle of a line without prefixing the line with a # will result in errors. For example, please ensure that none of the gene names (in the label column) have a # in them.

Missing values are coded as 'NA' (not 'na' - case matters) and values below background are coded as zero ("0")

There must be at least one label column. And columns for the same condition must be contiguous. Examples are given below for each analysis type.

Unpaired two-conditions data

For this type of analysis, where the first condition is a control, and second condition is an experimental, columns should be in this order:

    Label, ControlReplicate1, ControlReplicate2, ExperimentalReplicate1, ExperimentalReplicate2

Of course, you can have more than two control or experimental replicates, but they must be contiguous. You cannot have (for example) control columns, then experimental columns, the control columns again.

Here's an example file:

    # here's a comment
    # and another, and the line below is also a comment which is OK to insert
    # Label ContColumn1 ContColumn2 ExpColumn1 ExpColumn2
    # the real data starts just after this line 
    GH01040 0.81888287 0.98072154 1.16866872 1.38928931
    GH01059 0.87158715 0.9766095 1.05333957 1.18938903
    # comments can be interspersed as long as the line begins with a '#'
    GH01066 0.8881064 0.45129639 0.79107254 0.90903492
    GH01085 0.53412245 0.84194019 0.95338764 1.22393455

Paired two-conditions data

For paired data, you must upload raw measurements of two conditions with an equal number of replicates. Please see the Pairs Help Section for more details of when and why a Paired analysis is appropriate.

With raw measurements, columns should be in the following order:

    Label, Cond1Repl1, Cond1Repl2, Cond2Repl1, Cond2Repl2

This means that Cond1Repl1 will be paired with Cond2Repl1, and similarly Cond1Repl2 will be paired with Cond2Repl2. Of course, you can have more than two columns per condition, but the number of columns in each condition must be equal. The Unpaired two conditions data example file from above works as an example for this type of data.

Multiple conditions data

For this type of data, the columns for each condition should be contiguous. For example with three conditions having two replicates each, columns should be in the following order:

    Label, Cond1Repl1, Cond1Repl2, Cond2Repl1, Cond2Repl2, Cond3Repl1, Cond3Repl2

Again, you could have more than three conditions or more than two replicates each, but columns from the same condition need to be next to one another. Here is an example file:

    # here's a comment
    # and another, and the line below is also a comment which is OK to insert
    # Label Cond1Column1 Cond1Column2 Cond2Column1 Cond2Column2 Cond3Column1 Cond3Column2
    # the real data starts just after this line 
    GH01040 0.81888287 0.98072154 1.16866872 1.38928931 1.78923471 1.65654518
    GH01059 0.87158715 0.9766095 1.05333957 1.18938903 1.54621312 0.99854211
    # comments can be interspersed as long as the line begins with a '#'
    GH01066 0.8881064 0.45129639 0.79107254 0.90903492 1.46541311 1.64659878
    GH01085 0.53412245 0.84194019 0.95338764 1.22393455 0.89154451 0.87973211

Paired Analysis

The Paired (with ratios or differences) approach pairs a control value with an experimental value i.e. C1 with E1, C2 with E2, etc. The Unpaired (or ANOVA) approach does no such pairing. The difference is that if samples really are paired, the variance in the denominator can be much smaller (and hence power greater). The paired t-test evaluates whether the mean difference between paired samples is significantly different from zero, whereas the non-paired t-test tests if the mean of group 1 is different from the mean of group 2. Let's do a "classic" example.

Below is the body weight of a group of people before and after some diet regime was applied:

    PERSON      BEFORE          AFTER      DIFFERENCE

    Joe           200            180          -20
    Sue           120            100          -20
    George        175            155          -20

(Note: People here are like replicate experiments and Before and After are like Control versus Experimental). Doing a "paired t-test" results in showing the diet is very effective -- everyone loses 20 lb with no variance (that is: the mean difference is significantly different from zero). On the other hand, if we take the (Mean of the Afters) - (Mean of the Befores), the difference is still 20, however the variance within treatments is large so it is impossible to say the difference is significant.

Basically when observations are "paired" the paired approach is the correct and most powerful approach, when observations are not paired then we have to use the unpaired approach.

Minimum Non-zero Replicates Required

With the latest version of the Cyber-T library, even the extreme case of a single replicate can be handled with the Bayesian versions of the analyses. In these cases, the variance estimates are entirely determined by the background. If a single replicate in a condition is given, a warning message will be displayed.

Normalization and Low-Value Handling (Optional)

The statistical analyses performed by Cyber-T assumes that the data are approximately normal. This is often not the case with raw microarray (or other high-throughput) data. A common technique is to take the natural log (ln) of the data before processing. However, this approach has several drawbacks, mainly dealing with the inability to handle negative values. An alternative approach called VSN is based on the asinh transform and an assumption of a majority of genes being non-differentially expressed [12]. The webserver allows for pre-processing with optional low value thresholding or offsetting, and optional Log or VSN normalizations. If a Log or VSN normalization is chosen, some plots displaying the effect of the normalization are generated.

Posterior Probability of Differential Expression (Optional)

To interpret the results of a high-throughput data experiments, it is necessary to determine the global false positive and negative levels inherent in the data set being analyzed. We have implemented a mixture-model based method described by Allison et al. [13] for the computation of the global false positive and negative levels inherent in a DNA microarray experiment [6,8]. The basic idea is to consider the p-values as a new data set and to build a probabilistic model for these new data. When control data sets are compared to one another (i.e. no differential gene expression) it is easy to see that the p-values ought to have a uniform distribution between zero and one. In contrast, when data sets from different genotypes or treatment conditions are compared to one another, a non-uniform distribution will be observed in which p-values will tend to cluster more closely to zero than one.

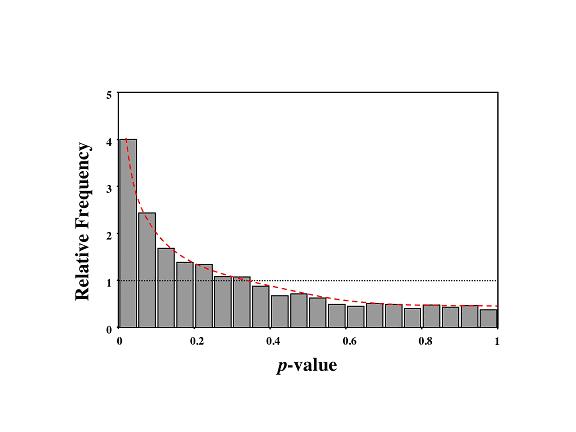
Distribution of the p-values from the lrp+ vs. lrp- data from Hung et al. [7]

The p-values, based on a regularized t-test distribution, of the 2,758 genes (lrp+ vs. lrp-) expressed at value above background in all replicate experiments grouped into 100 bins and plotted against the number of genes in each bin. The dotted line indicates the uniform distribution of p-values under conditions of no differential expression. The fitted model (dashed curve) is a mixture of a beta and the uniform distribution (dotted line).

That is, there will be a subset of differentially expressed genes with "significant" p-values. The computational method of Allison [13] is used to model this mixture of uniform and non-uniform distributions to determine the probability, PPDE(p) ranging from 0 to 1, that any gene at any given p-value is differentially expressed; that is, that it is a member of the uniform (not differentially expressed) or the non-uniform (differentially expressed) distribution. With this method, we can estimate the rates of false positives and false negatives as well as true positives and true negatives at any given p-value threshold, PPDE(<p). In other words, we can obtain a posterior probability of differential expression PPDE(p) value for each gene measurement and a PPDE(<p) value at any given p-value threshold based on the experiment-wide global false positive level and the p-value exhibited by that gene [6,8]. It should also be emphasized that this information allows us to infer the genome-wide number of genes that are differentially expressed; that is, the fraction of genes in the non-uniform distribution (differentially expressed) and the fraction of genes in the uniform distribution (not differentially expressed).

Multiple hypothesis testing correction (Optional)

Standard non-Bayesian methods to handle the situation addressed by the PPDE analysis above are to use Bonferroni or Benjamini & Hochberg multiple-hypothesis testing corrections to obtain q-values. Bonferroni q-values control the Family-Wise Error Rate (FWER) and Benjamini & Hochberg q-values control the False Discovery Rate (FDR). One could view these as a frequentist approach to the problem addressed by the PPDE analysis, or the PPDE analysis as the Bayesian treatment of the multiple hypothesis testing issue.

Parameters for the Bayesian Standard Deviation Estimation (Optional)

In calculating the Bayesian estimate of the standard deviation there are two different parameters that the user must set. These 2 parameters relate to setting the Bayesian estimate of variance derived from the observed population. The t-test is used to detect significant differences between the means of two groups relative to the observed variance within groups. In a perfect world, all micro-array experiments would be highly replicated within each experimental treatment. Such replication would allow accurate estimates of the variance within experimental treatments to be obtained and the t-test would then perform well. Microarray experiments are expensive and time consuming to carry out, and there is the possibility that both control and experimental tissues will be limiting. As a result, the level of replication within experimental treatments is often low. This results in poor estimates of within-treatment variance and a corresponding poor performance of the t-test itself. This problem can be solved addressed using a Bayesian statistical approach that incorporates prior information in the estimation of within gene within treatment variances.

Although in terms of strong inference there is really no substitute for proper experimental replication, in the case of microarrays many parallel pseudo-replicated experiments are carried out on any given microarray (i.e., one experiment for each gene). In particular, it is possible to use estimates of within-treatment variance from a number of genes of similar expression level to stabilize estimates of variance for any given gene. More precisely, the variance within any given treatment is estimated by the weighted average of a prior estimate of the variance for that gene (obtained from of local weighted average of the variance of other genes) and the experimental estimate of the variance for that gene. This weighting factor is controlled by the experimenter and will depend on how confident the experimenter is that the background variance of a closely related set of genes approximates the variance of the gene under consideration.

An important property of this Bayesian approach to consider is that in the two limiting cases of complete confidence in the prior and zero confidence in the prior, the Bayesian approach is equivalent to simply looking at fold change and testing differences between treatments using the simple t-test respectively. In the Bayesian approach the weight given to the within gene variance estimate is a function of the number of observations contributing to that value. This leads to the desirable property of the Bayesian approach converging to the t-test as the experimenter carries out additional replications and thus becomes more confident of the observed estimate of within treatment variance for any given gene.

1. Sliding Window Size

Indicates how wide you want the window surrrounding the point under consideration to be. This sample of the data provides an estimate of the average variability of gene expression for those genes that show a similar expression level. It is important to estimate this average from a wide enough level that it is accurate, but not so wide of a window so as to average in genes with too different of average expression level. A sliding window of 101 genes has been shown to be quite accurate when analyzing 2000 or more genes, with only 1000 genes a window of 51 genes may work better.

2. Bayes Confidence Estimate Value

This is a number from 0 to infinity that indicates the weight give to the Bayesian prior estimate of within-treatment variance. Larger weights indicate greater confidence in the Bayesian prior; smaller weights indicate more confidence in the experimentally observed variance. We have observed reasonable performance with the following rule of thumb: set the confidence such that the number of experimental observations plus the confidence is greater than 8.

If the confidence is left blank or zero, then a simple classical t-test is performed. If there is only a single replicate in a given condition, then the standard deviation estimates are completely determined by the prior, and a warning is issued to the user. If the confidence is set to zero and there is only a single replicate, we set a default confidence of 5 and issue a warning to the user.

One-way ANOVA and Post-hoc Tests

T-tests are appropriate for two-condition comparisons. However, with more than two conditions, for example, given three types of tissues, a one-way Analysis of Variance (ANOVA) is the proper way to handle the analysis.

In an ANOVA, the null-hypothesis is that all conditions come from the same distribution. Therefore, if for a given gene, we decide to reject the null-hypothesis (i.e., the p-value is below some significance threshold), then we can conclude that the gene is different across conditions. However, we cannot conclude anything about differences between any pair of conditions. For example, say we have tissue samples from the liver, the heart, and the lung. If for a given gene, the ANOVA p-value is less-than 0.5, we can conclude that the gene is differentially expressed between the three tissues. However, we cannot conclude that the gene is differentially expressed between the heart and the lung. To make this determination, we must use pairwise post-hoc tests. In essence, post-hoc tests examine differences across all pairs of conditions. Tukey's Honestly Significant Difference (TukeyHSD) and Scheffe's Method are available as post-hoc test options.

Note: the pairwise post-hoc p-values are not corrected for multiple testing. One should only examine pairwise post-hoc p-values for those measurements that are significant (after multiple testing correction) at the ANOVA level. Following this step-wise procedure should provide sufficient protection against Type I errors due to multiplicity. Low pairwise post-hoc p-values on their own are not indicitave of significant differential behavior.

Unpaired Two Conditions Data Analysis Output

Note: The 'C_#' and 'E_#' columns will have normalized data (if a normalization option was chosen). All calculated statistics use the data shown in the 'C_#' and 'E_#' columns.

Note: The input data is output in the downloadable text files. However it is NOT displayed in the web results.

• Lab_1 : Label column input by user
• ... : Possible more label columns
• C_1 : Control column #1 input by user
• C_2 : Control column #2 input by user
• ...
• E_# : Experimental column # input by user
• ...
• nC : The number of control observations
• nE : The number of experimental observations
• meanC : The mean of the control observations
• meanE : The mean of the experimental observations
• stdC : The standard deviation of the control observations
• stdE : The standard deviation of the experimental observations
• fold : The fold change between experimental and control, negative numbers indicate lower expression in the experimental
• rasdC : the background standard deviation for controls (if Bayesian analysis is performed)
• rasdE : the background standard deviation for experimentals (if Bayesian analysis is performed)
• bayesSDC : The Bayesian or regularized standard deviation of the control observations (if Bayesian analysis is performed)
• bayesSDE : The Bayesian or regularized standard deviation of the experimental observations (if Bayesian analysis is performed)
• T : The t-test statistic calculated from control and experimental data using the standard deviation (stdC, stdE) (if Bayesian analysis is NOT performed)
• DF : The degrees of freedom for the t-test statistic (nC+nE-2) (if Bayesian analysis is NOT performed)
• bayesT :: The t-test statistic calculated from control and experimental data using the Bayesian standard deviation (bayesSDC, bayesSDE) (if Bayesian analysis is performed)
• bayesDF : The degrees of freedom for the t-test statistic plus that associated with the Bayesian estimate (if Bayesian analysis is performed)
• varRatio : The ratio of the variances of the control and experimental treatments
• pVal : The p-value associated with the t-test on control and experimental data (column T or bayesT) with DF or bayesDF degrees of freedom
• cum.ppde.p : The posterior probability of differential gene expression [PPDE(<p)] given a threshold for p between control and experimental (if PPDE analysis is performed)
• ppde.p : The posterior probability of differential gene expression [PPDE(p)] between control and experimental (if PPDE analysis is performed)
• ROC.x : x-coordinates for ROC plot based on PPDE analysis (if PPDE analysis is performed)
• ROC.y : y-coordinates for ROC plot based on PPDE analysis (if PPDE analysis is performed)
• Bonferroni : Bonferroni corrected q-values (if multiple hypothesis testing correction is performed)
• BH : Benjamini & Hochberg corrected q-values (if multiple hypothesis testing correction is performed)

Paired Two Conditions Data Analysis Output

Note: The 'R_#' columns will have normalized data (if a normalization option was chosen). All calculated statistics use the data shown in the 'R_#' columns.

Note: The input data is output in the downloadable text files. However it is NOT displayed in the web results.

• Lab_1 : Label column input by user
• ... : Possible more label columns
• R_1 : Ratio column #1 input by user
• R_2 : Ratio column #2 input by user
• ...
• nR : Number of ratios
• meanR : Mean of the log transformed ratios
• stdR : Standard devation of the ratios
• rasdR : the background standard deviation for ratios (if Bayesian analysis is performed)
• bayesSD : The Bayesian or regularized standard deviation of the ratios (if Bayesian analysis is performed)
• ttest :: The t-test statistic calculated from ratios data using either stdR or bayesSD
• DF : The degrees of freedom for the t-test statistic (nR-1) (if Bayesian analysis is NOT performed)
• bayesDF : The degrees of freedom for the t-test statistic plus that associated with the Bayesian estimate (if Bayesian analysis is performed)
• pVal : The p-value associated with the t-test on ratios (column ttest) with DF or bayesDF degrees of freedom
• cum.ppde.p : The posterior probability of differential gene expression [PPDE(<p)] given a threshold for p between control and experimental (if PPDE analysis is performed)
• ppde.p : The posterior probability of differential gene expression [PPDE(p)] (if PPDE analysis is performed)
• ROC.x : x-coordinates for ROC plot based on PPDE analysis (if PPDE analysis is performed)
• ROC.y : y-coordinates for ROC plot based on PPDE analysis (if PPDE analysis is performed)
• Bonferroni : Bonferroni corrected q-values (if multiple hypothesis testing correction is performed)
• BH : Benjamini & Hochberg corrected q-values (if multiple hypothesis testing correction is performed)

This shows the output of the mixture model parameters from running the PPDE module. See the PPDE paper for more details [13].

Graphical Results

The plots output will depend on the type of analysis and input parameters. The titles and labels of the plots are largely self-explanatory. Possible plots include:

• Control Vs. Experimental Scatterplots (before and after normalization).
• Plots of standard deviation of the expression levels versus the corresponding mean, visually answering the question: Is there more variation at higher values of expression? This is done for different conditions and normalizations.
• A Receiver Operating Characteristic (ROC) curve which depicts the tradeoff between false positives and true positives when choosing a p-value threshold for PPDE.

There are two plotting options:

• Plot using density estimate smoothing : Plots will have data binned and colored to show smooth density estimates. This allows the user to see the distribution of the data.
• Remove outliers: Produces plots where outliers (more than 2 IQR above or below the 1st or 2nd quantiles, respectively) have been removed. This allows the user to see the true relationship by plotting most of the data in a reasonable scale.

R's (distributed) home, the Comprehensive R Archive Network (CRAN)

References

1. Baldi, P. and Long, A.D., "A Bayesian Framework for the Analysis of Microarray Expression Data: Regularized t-Test and Statistical Inferences of Gene Changes", Bioinformatics, 17, 6, 509-519, (2001).
2. Choe, S.E., Boutros, M., et al, "Preferred analysis methods for Affymetrix GeneChips revealed by a wholly defined control dataset", Genome Biology, 6:R16 (2005)
3. Zhu, Q., Miecznikowski, J.C., and Halfon, M.S., "Preferred analysis methods for Affymetrix GeneChips. II. An expanded, balanced, wholly-defined spike-in dataset", BMC Bioinformatics, 11, 285. (2010).
4. Murie, C., Woody, O., et al, "Comparison of small n statistical tests of differential expression applied to microarrays", BMC Bioinformatics, 10, 45 (2009).
5. Dondrup, M., Hüser, A.T., et al, "An evaluation framework for statistical tests on microarray data", Journal of Biotechnology, 140 (1-2):18-26 (2009).
6. Baldi, P. and Hatfield G.W., "DNA Microarrays and Gene Expression : From Experiments to Data Analysis and Modeling", Cambridge University Press (2002).
7. Hung, S.P., Baldi, P., and Hatfield G.W., "Global gene expression profiling in Escherichia coli k12" Journal of Biological Chemistry, 277, 40309-40323 (2002).
8. Hatfield, G.W., Hung, S., and Baldi, P., "Differential Analysis of DNA Microarray Gene Expression Data", Molecular Microbiology, 47:871-877 (2002).
9. Sundaresh, S., Doolan, D.L., et al, "Identification of humoral immune responses in protein microarrays using DNA microarray data analysis techniques", Bioinformatics, 22(14), 1760-6 (2006).
10. Crompton, P.D., Kayala, M.A, et al, "A prospective analysis of the Ab response to Plasmodium falciparum before and after a malaria season by protein microarray" Proceedings of the National Academy of Sciences of the United States of America, 107(15):6958–63, April 2010.
11. Kaake, R.M., Wang, X., and Huang, L., "Profiling of protein interaction networks of protein complexes using affinity purification and quantitative mass spectrometry", Molecular & cellular proteomics : MCP, 9(8), 1650-65 (2010).
12. Huber, W., von Heydebreck, A., et al, "Variance stabilization applied to microarray data calibration and to the quantification of differential expression", Bioinformatics, 18 Suppl 1, S96-104 (2002).
13. Allison, D.B., Gadbury, G.L., et al, "A mixture model approach for the analysis of microarray gene expression data", Computational Statistics & Data Analysis, 39:1-20 (2002).
14. Kayala, M.A. and Baldi, P., "Cyber-T web server: differential analysis of high-throughput data", Nucleic Acids Research, 40 (W1): W553-W559 (2012)